Schemes of Learning
Vision
In Maths, we aim to …
- inspire positive attitudes towards the subject and awareness of the relevance of mathematics in the real world
- create competence and confidence in using and applying mathematical knowledge, concepts and skills
- develop an ability to solve problems, to reason, to think logically and to work systematically and accurately
- encourage initiative and motivation to work both independently and in cooperation with others
- promote confident communication of maths where pupils ask and answer questions, openly share work and learn from mistakes
- support an ability to use and apply mathematics across the curriculum and in real life
- nurture an understanding of mathematics through a process of enquiry and investigation.
We aim to provide a stimulating and exciting learning environment that takes account of different learning styles and uses appropriate resources to maximise teaching & learning.
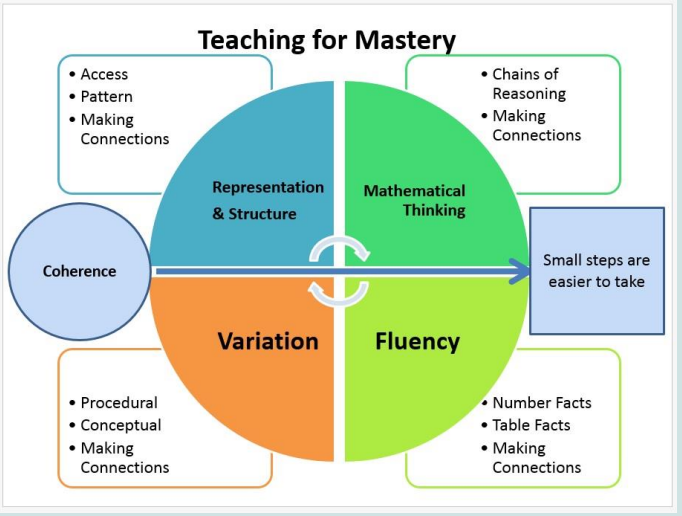
At Catcott Primary, we are currently working towards embedding the ‘Teaching for Mastery’ approach. Our Teaching for Mastery is underpinned by the NCETM’s 5 Big Ideas as well as working collaboratively with the White Rose Scheme.
-Opportunities for Mathematical Thinking allow children to make chains of reasoning and connections with the other areas of mathematics.
-A focus on Representation and Structure ensures concepts are explored using concrete, pictorial and abstract representations. This includes actively looking for patterns and generalisations that underpin sets of numbers and ‘laws’ .
-Coherence is achieved through the planning of small, connected steps to link every question and lesson within a topic. The curriculum is broken into small steps to develop mastery and address all aspects in a logical progression. This will ensure deep and sustainable learning for all pupils.
-Teachers use both procedural and conceptual Variation within their lessons and there remains an emphasis on Fluency with a relentless focus on number, the quick recall of facts and procedures, the flexibility and fluidity to move between different contexts and representations of mathematics
